High-Frequency Transistorized Function Generator
The FGC-200 is a credit card-sized function generator capable of generating waveforms up to 40 MHz. Its only active devices are discrete transistors.
This project is an exercise of integrated style circuit design. As of today (2017), integrated circuits on silicon remain too expensive for tinkering, so discrete bipolar-junction transistors on a printed circuit board were used in this project. In addition to the choice of using discrete transistors, monolithic design techniques and limitations, such as bandgap compensation and a lack of coupling capacitors, were used to stay true to the spirit of integrated circuits.
Description
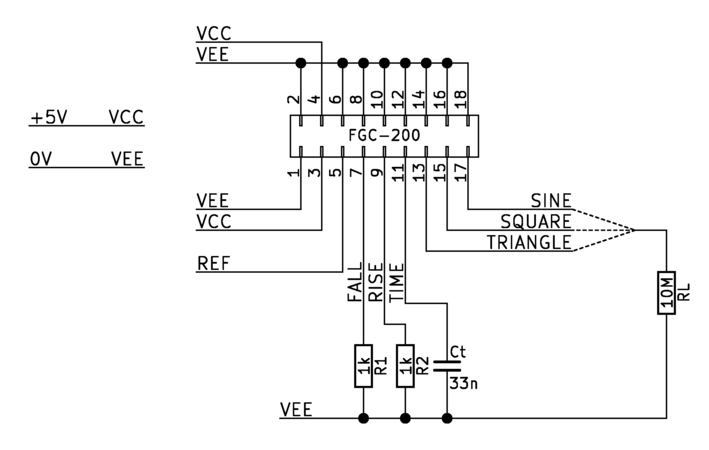
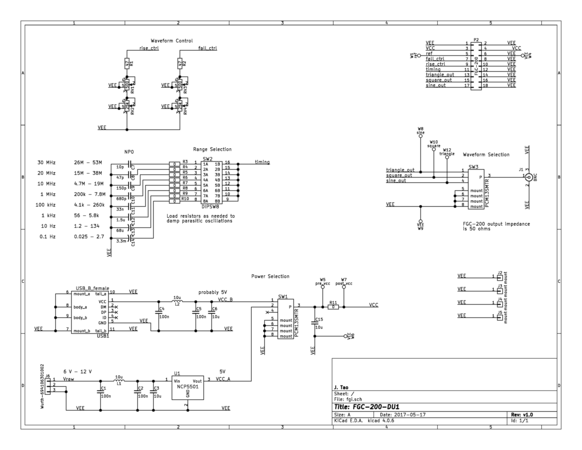
The FGC-200 is a transistorized function generator capable of generating high-frequency triangle, square, and sine waveforms. The output waveform frequency can be controlled from 0.1 Hz to 40 MHz with a capacitor and two resistors in conjunction with an internal 1.245 V bandgap voltage reference. Because the function generator uses a bandgap voltage reference for its internal circuitry, its frequency and waveform characteristics are resistant to changes in temperature and power supply. The circuit can be used with a supply voltage as low as 5 V and consumes approximately 100 mA.
The output waveform symmetry can be varied through the ratio of the two frequency-control resistors. Advanced frequency control, such as sawtooth waveform generation, pulse width modulation, and frequency modulation, is implemented by using current source equivalent circuits in place of the two frequency-control resistors.
The triangle, square, and sine waveforms are output through three independent output buffers. The output for all waveforms is 1 VP-P, symmetrical around 2.0 V from ground. Each output stage is capable of sourcing or sinking up to 200 mA through their internal 50 Ω source terminations.
Electrical Characteristics
Conditions unless otherwise specified:
VEE = 0 V,
VCC = 5 V,
IREF = 0 A,
R1 = R2 = 1.00 kΩ,
Ct = 33 nF,
RL = 10 MΩ
| PARAMETER | SYMBOL | CONDITIONS | MIN | TYP | MAX | UNITS |
|---|---|---|---|---|---|---|
| FREQUENCY CHARACTERISTICS | ||||||
| Maximum Operating Frequency | F | Ct = board, R1 = R2 = 68 Ω
RL = 50 Ω |
40 | MHz | ||
| Frequency Programming Current | IP1, IP2 | 0.02 | 20 | mA | ||
| Symmetry Adjustment | ADJSYM | 10 | 90 | % | ||
| Maximum Modulating Frequency | FMOD | 4 | MHz | |||
| Programming Reference Voltage | VP1, VP2 | 1.145 | 1.245 | 1.345 | V | |
| Freq. Power Supply Rejection | (ΔF/F0) / ΔVCC | VCC = 4.7 to 9.7 V | 0.44 | %/V | ||
| OUTPUT BUFFER (TRIANGLE, SQUARE, SINE) | ||||||
| Offset | VOFFSET | 1.9 | 2.0 | 2.1 | V | |
| Output Resistance | ROUT | 49.5 | 50 | 50.5 | Ω | |
| Maximum output current | IOUT | ±200 | mA | |||
| TRIANGLE-WAVE OUTPUT | ||||||
| Amplitude | VOUT | 0.7 | 1.0 | 1.4 | VP-P | |
| SQUARE-WAVE OUTPUT | ||||||
| Amplitude | VOUT | 0.9 | 1.0 | 1.1 | VP-P | |
| Rise Time | tR
| 10% to 90%, RL = 50 Ω |
| 8 |
| ns |
|
| Fall Time | tF | 90% to 10%, RL = 50 Ω | 9 | ns | ||
| SINE-WAVE OUTPUT | ||||||
| Amplitude | VOUT | 0.9 | 1.0 | 1.1 | VP-P | |
| VOLTAGE REFERENCE | ||||||
| Output Voltage | VREF | 1.145 | 1.245 | 1.345 | V | |
| Ref. Power Supply Rejection | ΔVREF / ΔVCC | VCC = 4.7 to 9.7 V | -0.2 | mV/V | ||
| POWER SUPPLY | ||||||
| Supply Voltage | VCC | 4.6 | 5.0 | 15 | V | |
| Supply Current | ICC | 100 | mA | |||
Typical Operating Characteristics
All of the following waveforms were measured with 100 MHz bandwidth. The measurements were made through through a 50Ω coaxial cable from the FGC-200 to the oscilloscope.
500 Hz
The following 500 Hz waveforms are measured with a 10 MΩ termination and are displayed with 0.5 ms/div, 0.2 V/div.
25 MHz
The following 25 MHz waveforms are measured with a 50 Ω termination and are displayed with 0.01 us/div, 0.1 V/div.
40 MHz
The following 40 MHz waveforms are measured with a 50 Ω termination and are displayed with 5 ns/div, 0.1 V/div.
Ramp
The following ramp waveforms are measured with a 10 MΩ termination and are displayed with 50 us/div, 0.2 V/div.
Frequency Modulation and Edges
The following frequency modulated waveform is measured with a 50 Ω termination and is displayed with 20 us/div, 0.1 V/div. The modulating input is a 5 Vpp square wave displayed with 5 V/div on the same time base.
The following rising and falling edge waveforms are measured with a 50 Ω termination and are displayed with 5 ns/div, 0.1 V/div.
Pin Description
| PIN | NAME | FUNCTION |
|---|---|---|
| 1, 2, 6, 8, 10, 12, 14, 16, 18 |
VEE | Ground |
| 3, 4 | VCC | Power supply |
| 5 | REF | Bandgap voltage reference |
| 7 | FALL | Waveform falling edge control |
| 9 | RISE | Waveform rising edge control |
| 11 | TIME | External timing capacitor |
| 13 | TRIANGLE | Triangle wave output |
| 15 | SQUARE | Square wave output |
| 19 | SINE | Sine wave output |
Application Description
Current flowing from the FALL and RISE pins are used to respectively charge and discharge the timing capacitor Ct on the TIME pin. The function generator alternately applies those currents to the capacitor to produce a voltage triangle wave, from which the square wave and sine wave outputs are derived.
The period of the generated waveform is equal to the time it takes for the capacitor's voltage to rise and fall 1 VP-P. In this way, the currents on the FALL and RISE pins (I1 and I2) control the waveform's rising and falling time, which define the waveform's period. Thus, these two currents control the frequency of the waveform. This relationship is elaborated in the later section "Description of Frequency from a Schmitt Trigger Oscillator." With f as the output frequency, let C be the timing capacitor's value and V be the VP-P of the generated waveform.
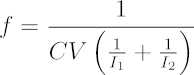
If the programming currents I1 and I2 are equal,
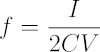
A caveat of applying the timing capacitor is that it produces unintended oscillation. Parasitic inductance of the conductor from the capacitor to the function generator combined with the self resonance of the capacitor contribute to this oscillation. A simple remedy is to place a damping resistor in series with the timing capacitor to supress the oscillation.
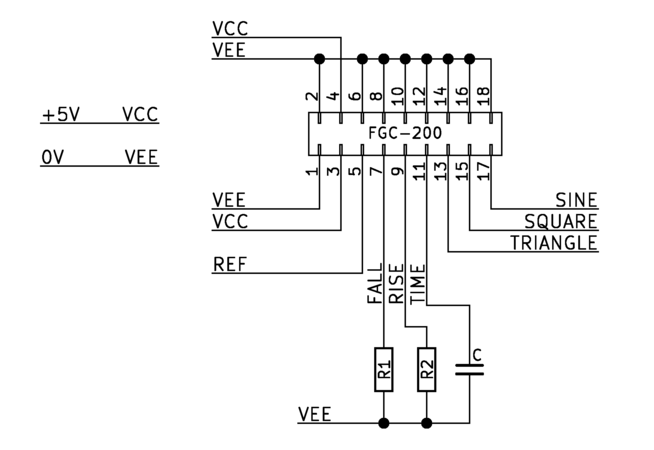
Resistive Programming
The waveform can be programmed by placing resistors on the FALL and RISE pins to ground (VEE). The current flowing through the resistors is determined by the bandgap referenced voltage at the pins and the values of the resistances. In general, current I = VREF / R, where VREF = 1.245 V and R is the programming resistor.
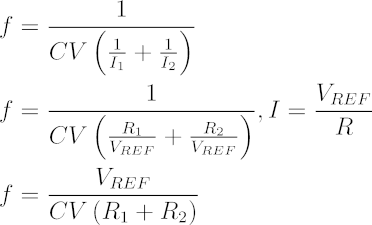
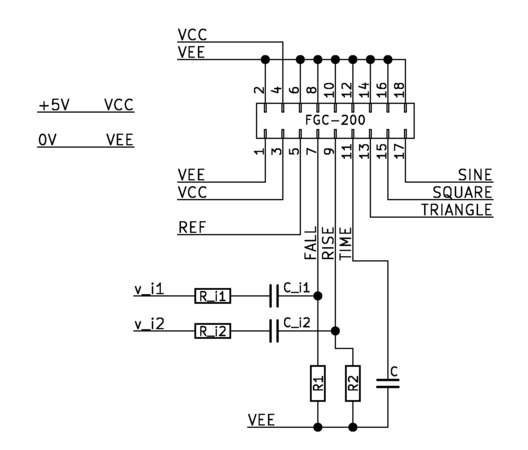
AC-Coupled Control
The circuit to resistively program the function generator can be modified to provide electronic waveform control with the addition of capacitors. The low impedance FALL and RISE pins can receive a small signal current as an input with this modification. With the small signal current input i, let vi be the small signal input voltage and ri be the controlling input resistor. Meanwhile, the capital letters of I, VREF, and R represent the static bias conditions.
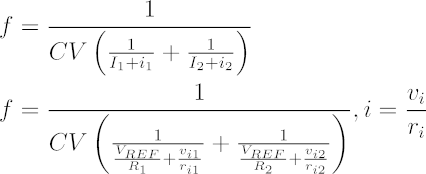
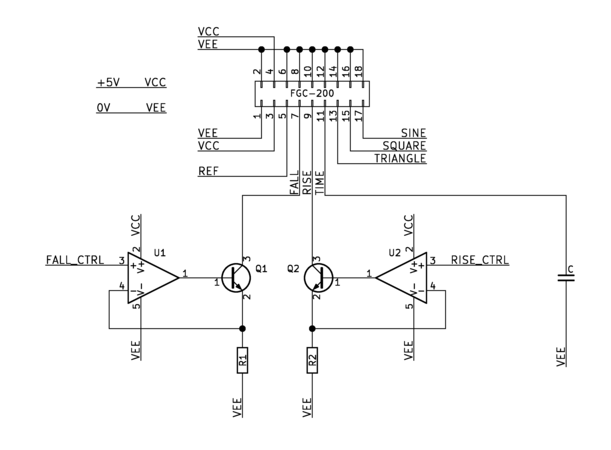
Direct Couple Control
The resistive programming can be replaced with transistors to provide direct control to carry out relatively slow frequency functions such as frequency sweeping or duty cycle adjustment. The transistors can be placed on the FALL and RISE pins in common-emitter configuration with degeneration. This circuit is a transconductance amplifier whose current outputs are fed to the input pins. Operational amplifiers can be added to improve the linearity of the control.
Example Application Circuit
The FGC-200-DU1 demonstration unit provides simple user interface for the function generator to demonstrate its functions and performance.
Story Time: Beginnings of the Function Generator
I wanted to make a function generator because it seemed like a good project that would take me back to the basics. The project allowed me to focus on the methods it took to design one rather than the final result.
There are simple ways to build a simple function generator, such as with opamps, 555 IC timers, or monolithic function generator ICs (essentially building a function generator with a function generator). However, I wanted a performant solution that I could actually design and build myself. As a result, I aspired to build a function generator that would be comparable to the reknown MAX038 IC or the HP3112A function generator, the type I had used in my university labs. Not only that, I wanted build it entirely with transistors as if it was an integrated circuit.
This project's topology was inspired by a final exam from a communication electronics class at university. The particular exam problem that inspired this project was one that explored waveform control with a schmitt trigger oscillator where a timing capacitor was charged with arbitrary currents. This method allows both fine waveform shape control with frequency control in a single circuit. The circuit was something I felt I needed to see for real.
Requirements
The requirements I set forth to achieve was a function generator that could generate triangle, square, and sine waves. The circuit should also reach at least 20 MHz and have waveform shape control, namely for rising and falling edge rate (this also provides duty cycle and frequency modulation capabilites). I also wanted the frequency to be somewhat immune to temperature and power supply changes. Finally, the circuit was to operate on 5 V so that I could easily use the circuit with other circuits and have moderate power consumption.
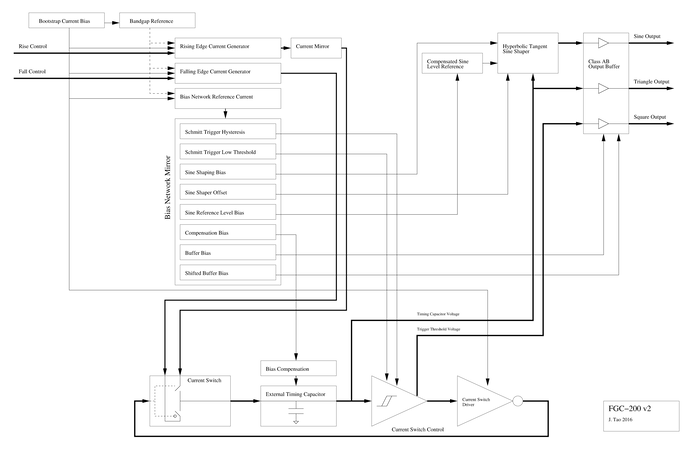
Detailed Circuit Description
The core of this function generator is an RC oscillator. The oscillator is built on a fast schmitt trigger and a bandgap voltage reference that produces stable biasing and control. The oscillator produces both triangle and square waveforms. The function generator uses an over driven differential pair for shaping the triangle waveform into an approximated sine waveform. The output stages are class AB push-pull buffers.
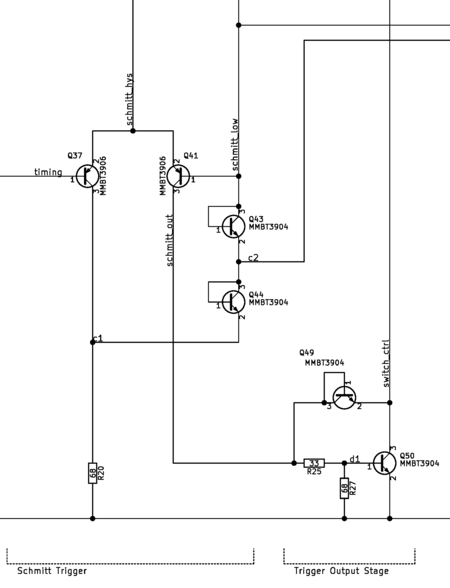
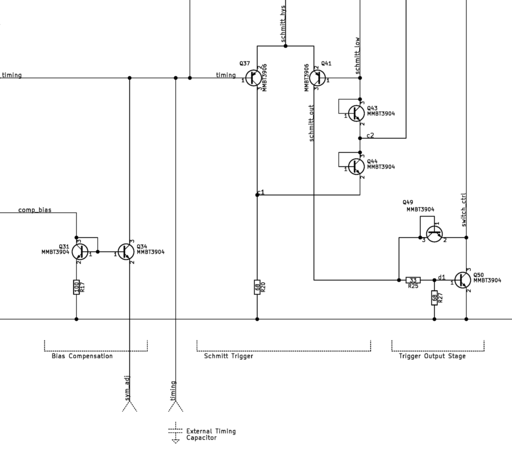
Schmitt Trigger Oscillator
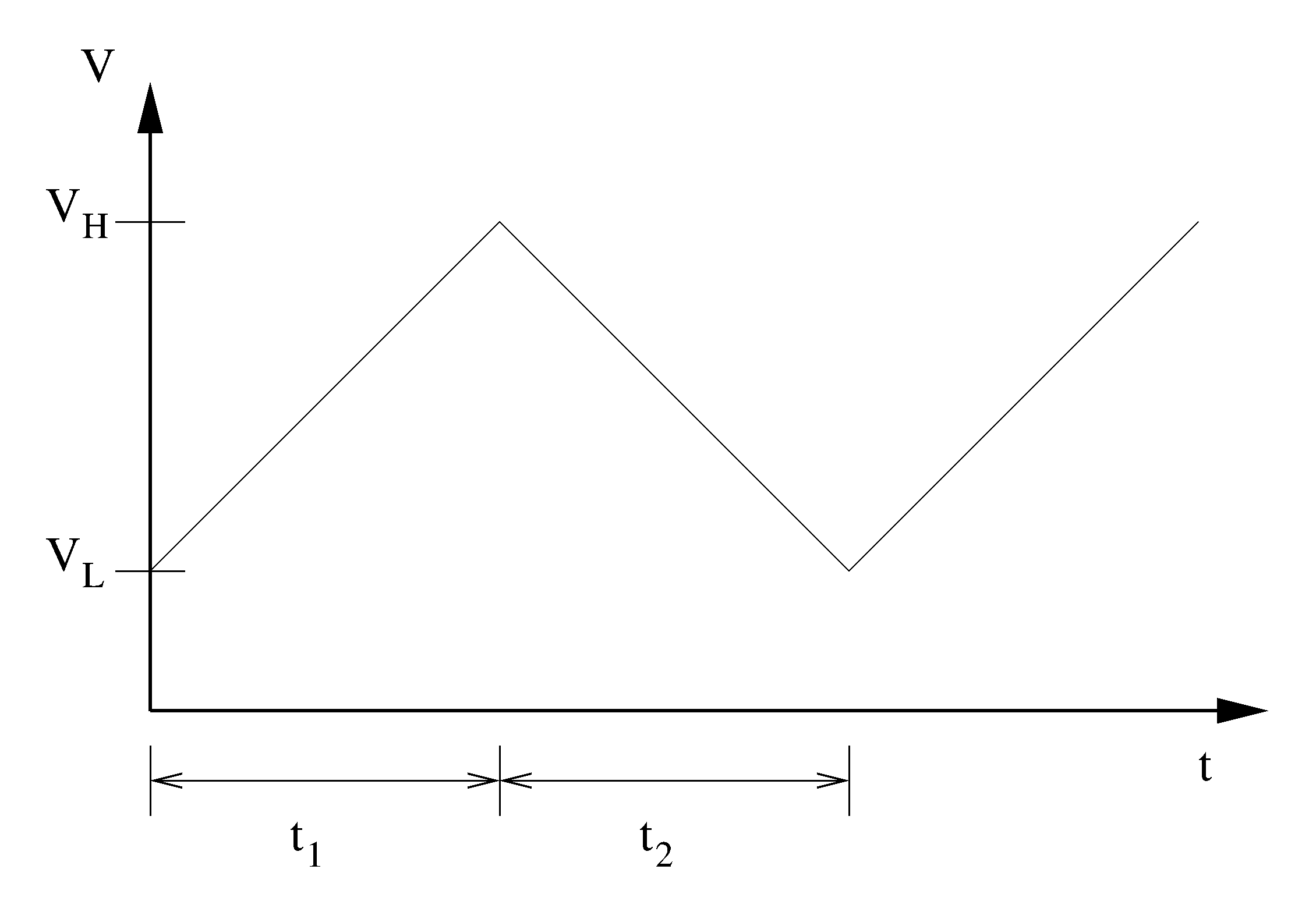
The function generator uses a Schmitt trigger oscillator, which operates by alternating between two voltage thresholds and charging a timing capacitor accordingly. When the schmitt trigger sees that the capacitor's voltage has reached the low threshold, the schmitt trigger begins charging the capacitor and starts looking for when the voltage reaches the high threshold. The trigger discharges the capacitor when the capacitor's voltage reaches the high threshold, and then the cycle repeats. This charging-discharging action produces a triangle wave across the timing capacitor.
Description of Frequency from a Schmitt Trigger Oscillator
The generatred waveform's shape and frequency are defined by the timing capacitor and the currents used to charge and discharge the capacitor.
The definition of a capacitor can describe the time it takes for a capacitor to charge a certain amount of voltage (ΔV = VH - VL), given a constant charging current.
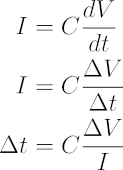
The period of the triangle waveform is the time it takes for the voltage on the capacitor to rise (t1) and fall (t2). The capacitor is charged by a current I1 and discharged by a current I2. We can substitute the times with the description derived from the definition of capacitance. Note that the times and voltages in the following equations are assumed to be differences.
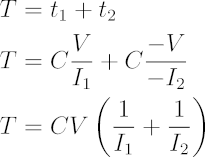
From the period, we obtain frequency.
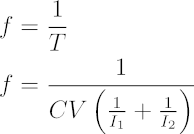
If the charging and discharging currents are the same (I = I1 = I2), the resulting triangle waveform on the capacitor is symmetric. In this case, the frequency equation can be simplified further.
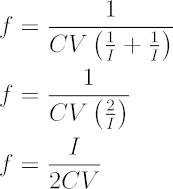
Implementation of the Schmitt Trigger
The advantage of this type of oscillator is the low number of external components needed while retaining controllability of waveform shape and frequency. With this topology, no inductor is needed as with resonant circuit oscillators. Also, controllability implies stable frequencies and amplitude, provided that the source of control is stable as well. In the case of this project, a bandgap voltage reference provides that stable control.
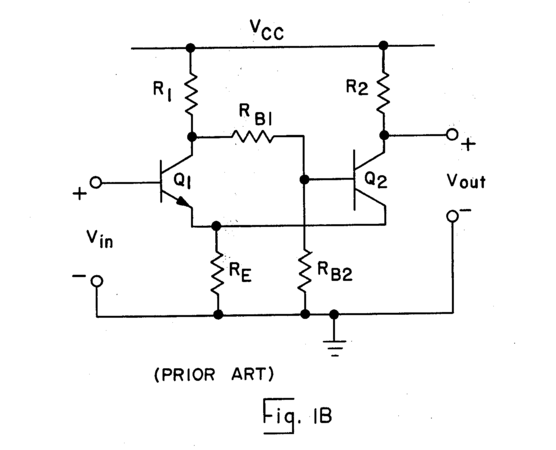
The Schmitt trigger of this function generator is a single ended trigger built on a transistor pair. It is inspired by the prior art schmitt triggers in the figures of US Patent US4219744 A[1]. My trigger design began its life as the exact circuit in Figure 1B of the patent. I replaced the resistors in the design with active transistors to improve designability and control, although it introduced non-idealities from transistor biasing and temperature. There are more advanced topologies, but I wanted something simple enough to build and something that operated with low voltages.
Combatting Temperature Changes
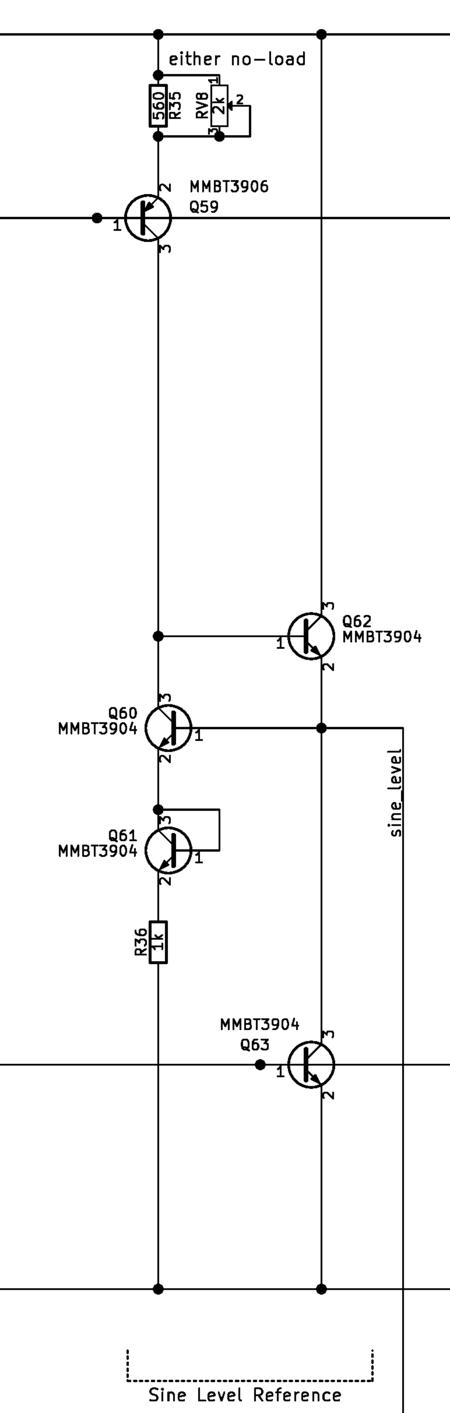
In my Schmitt trigger, the high and low thresholds are set by reference currents, the single resistor R20, and multiple level shifts diode in the feedback loop. The low-input threshold is determined by the voltage across the reference resistor R20 created by the current source on the schmitt_low net of the feedback loop plus the voltage drops from the level shift diodes. When the trigger is triggered at the low threshold, the resistor sees an increase in current equal to the differential pair's tail current, which shifts the trigger's threshold to the high-input threshold. The hysteresis sets the output waveform's amplitude and frequency. Tight control of this hysteresis is critical to obtaining stable results with the function generator.
Stable current sources are needed to produce a stable hysteresis that the critical to the performance for the function generator. In this project, the reference currents are provided through a bandgap referenced bias network to resist changes in temperature and power supply. Unfortunately, the level shift diodes have a forward voltages that change with temperature. This disturbance was not compensated in this project, since they only affect the offset of the generated waveform from ground, a less important aspect of the waveform. As long as the schmitt trigger's hysteresis is stabilized, the generated waveform's frequency and amplitude would also be stabilized.
Output Stage
The output stage of the Schmitt trigger is designed with fast switching speed in mind. The stage is a TTL-style output stage with an active load in the form of a Wilson current mirror. The output driver in the bottom portion of this stage uses a voltage clamping diode (diode connected transistor) to prevent the driving transistor from becoming fully saturated. This feature improves switching speed by avoiding saturation to prevent charge storage in the base of the driving transistor. This technique is commonly known as a Baker clamp or found in the form of a Schottky transistor.
The top half of the output stage is an active load to complement the bottom driving portion. This Wilson mirror load replaces the simple resistive load found in typical TTL circuits. The active load presents a very high output impedance, which improves switching speed in addition to the saturation clamp.
Despite fast speeds from the topology of the output stage, the design is not without detriments. The output stage is asymmetric in that it can sink up to 200 mA (limit of the transistor) while only being capable of sourcing about 20 mA (limited by design around power consumption). This asymmetry causes the rising and falling edge times to be different depending on the current to be sourced or sunk. This asymmetric switching behavior is exacerbated with increased frequency, because the output stage needs to source or sink more current to generate higher frequencies.
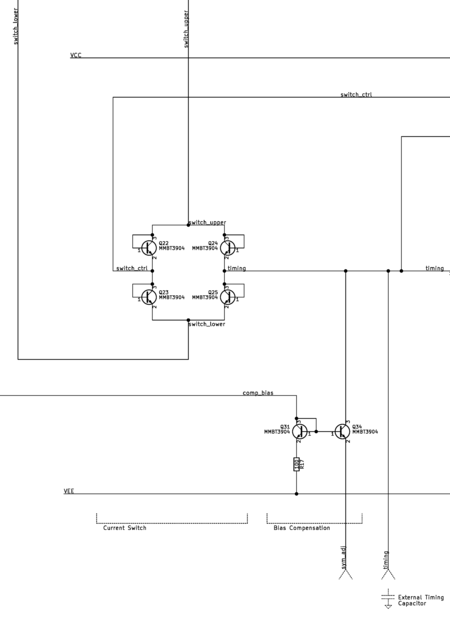
Bias Compensation
The bias compensation circuit compensates for the trigger's bias current. The BJT that forms the input of the trigger injects its base bias current into the timing capacitor. The extra current from the base causes asymmetry in the waveform where the rising edge is faster than the falling edge. In addition to asymmetry, the extra current reduces the tuning range of the function generator at the low frequencies. In the case where the inteded charge and discharge currents are zero, the capacitor's voltage would slowly climb due to the extra base current. Eliminating the extra current would lower the minimum possible frequency.
In the function generator, the extra base current is not reduced but redirected away from the capacitor by the bias compensation circuit. The circuit sinks the base current so that the current does not contribute to the timing capacitor's voltage. Since the current depends on transistor characteristics that vary with manufacturing, the current to be sunk needs to be tuned after the function generator is assembled.
Current Switch
The current switch is a simple diode switch bridge that can be constructed with only four diodes. A similar diode switch can be found in classic function generators such as the HP3312A. This current switch is used in conjunction with sourcing and sinking current sources to charge and discharge the timing capacitor.
From a perspective using current, the current switch relies on the control signal to provide the current to satiate either of the programmed current sources so that only one of the programmed current sources sink from or source to the output. When the control signal is sourcing current, current can only flow to the bottom current source. Because of the high impedance of the lower current source, the voltages naturally work out to shut off the top-left and bottom-right portions of the bridge. As a result, current only flows in the top-right and bottom-left portions. When the control signal sinks instead of sources current, these portions of the diode bridge swap roles and current flows in the top-left and bottom-right portions.
From a perspective using voltage, the control signal changes the biasing of the diodes to provide alternate paths for current to flow. The controlling input voltage is referenced to the voltage of the capacitor. To source current into the capacitor, the input voltage must be at least VF (diode's forward active voltage) higher than the capacitors voltage. To sink current from the capacitor, the input voltage must be at least VF lower than the capacitor's voltage.
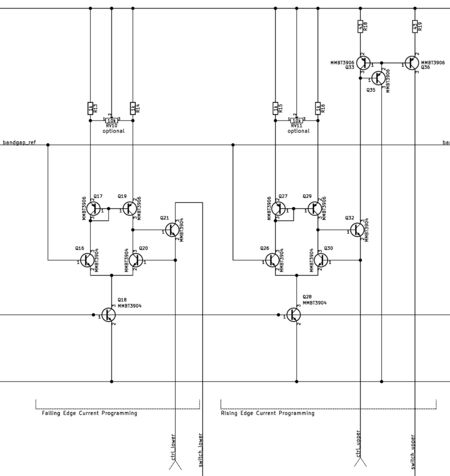
Frequency Control Current
Two transconductance amplifier provide the frequency control current to charge and discharge the timing capacitor. These amplifiers are aways on, and the current switch determines which amplifier's current is used for the timing capacitor. The amplifiers are identical apart from the current mirror on the rising edge control amplifier to flip the current direction from sinking to sourcing.
From a high level point of view, the amplifiers are op-amps that buffer the internal reference voltage through a transistor in common-base configuration. The common-base transistor buffers the user's input current to the timing capacitor. This configuration provides a good frequency response, suitable for modulating input with both small and large signals.
The transconductance amplifiers accept either a resistance or current as its input. The amplifiers act as current buffers with a low impedance input. The input also outputs the same voltage as the bandgap referenced voltage, which can be used with an external resistance to create a current that is independent of power supply changes. That derived current from the extermal resistance is intrinsically buffered by the amplifier. In this way, the current controls can accept either a user's resistances or high impedance current sources.
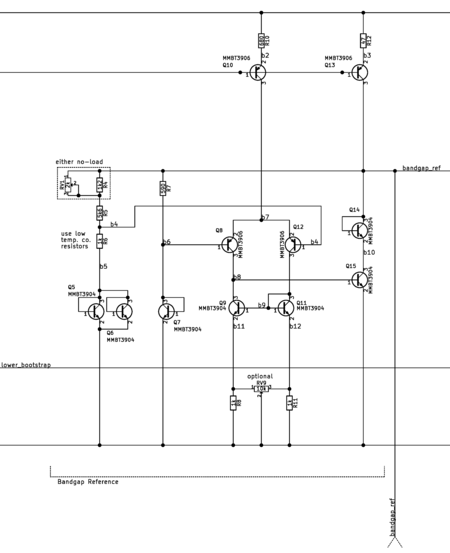
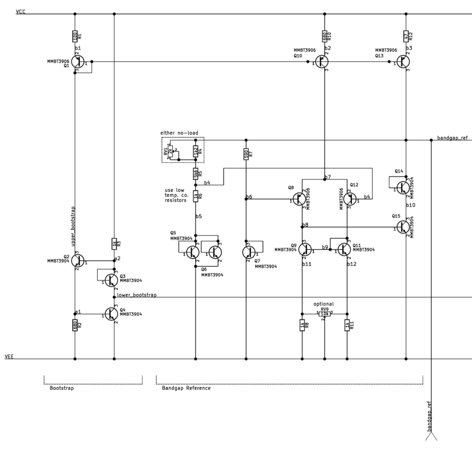
Bandgap Voltage Reference Generator
Bandgap voltage references are circuits that use the inherent temperature sensitivity of semiconductors to compensate for temperature changes in other semiconductors. Through this technique, the output voltage of the reference becomes based on the semiconductor's bandgap voltage, a fundamental constant of nature. Non-idealities cause some deviation from this voltage in actual implementation, but the resulting voltage from implementation is still somewhat stable with temperature.
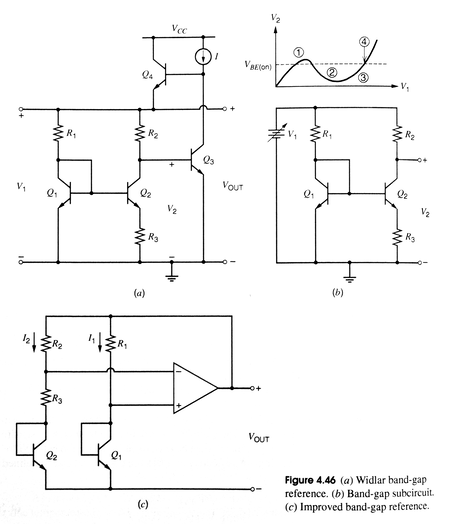
In this function generator, the bandgap voltage reference topology is a textbook design. The reference generator uses two reference components with different current-voltage relationships and similar thermal sensitivity. A transistorized op-amp examines the difference between the two components and produces a reference voltage. The reference voltage is solely derived from the difference in the components' current-voltage relationships, independent of temperature. A temperature coupling caveat is discussed in the PCB design section.
The textbook's description of the voltage reference mentions a starting condition problem. The two reference components remain off if they are off, because this state satisfies the same requirements that causes the op-amp to produce the reference voltage. The textbook does not provide a solution for this, because it is the responsibility of the op-amp, not the reference components, to handle this edge case. My solution was to shift the op-amp's output voltage with transistor Q14 so that the op-amp's output saturates against the ground rail earlier to prevent it from manipulating the reference components too early.
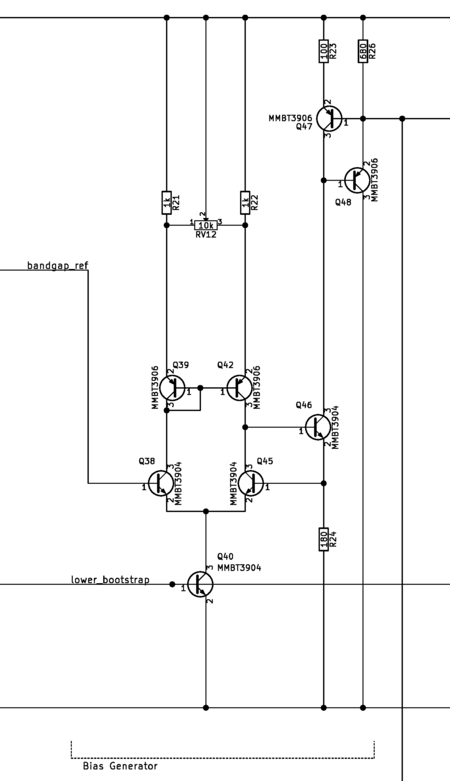
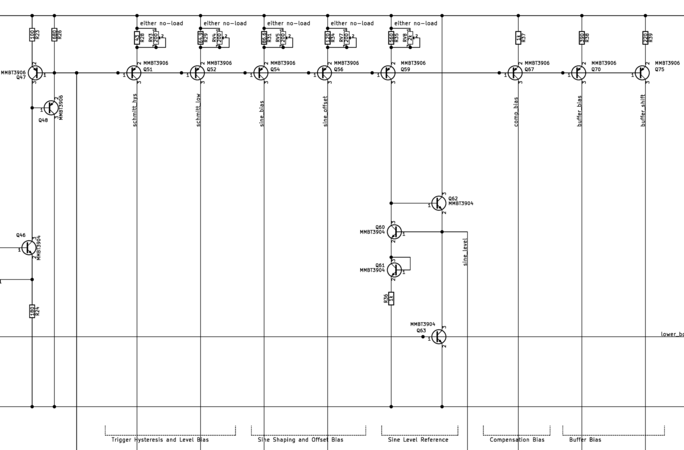
Bias Network
The function generator relies on the bias network, which is stabilized by the bandgap voltage reference. The bias network consists of a bootstrap circuit, a bias current generator, and a bias distribution section.
The bootstrap circuit provides an initial imprecise current to start up the bandgap voltage reference generator and the tail currents to run other transistorized op-amps. Although the generated current is imprecise, it can still be used to bias differential circuits without too much trouble. The current it generates is proportional to the base-emitter voltage VBE, which decreases about 2 mV/K, independent of power supply variations.
The bias current generator provides the main reference current from which all other bandgap-referenced currents are derived. The generator is a transconductance amplifier that applies the bandgap reference voltage over a current-programming resistor to produce the main current. This current is then used via a current mirror to produce the different currents used throughout the circuit
The bias distribution is a giant current mirror that derives different current "taps" from the main reference current. The current mirror uses emitter degeneration to derive the currents. For large emitter degeneration resistors, the derived currents only depend on the ratio of resistors and the main reference current. The bias distribution mirror also uses a beta helper transistor and a decoupling capacitor inside to decrease coupling between the different taps. The beta helper adds some gain error, which is tolerable since I was looking to only gaining independence from temperature.
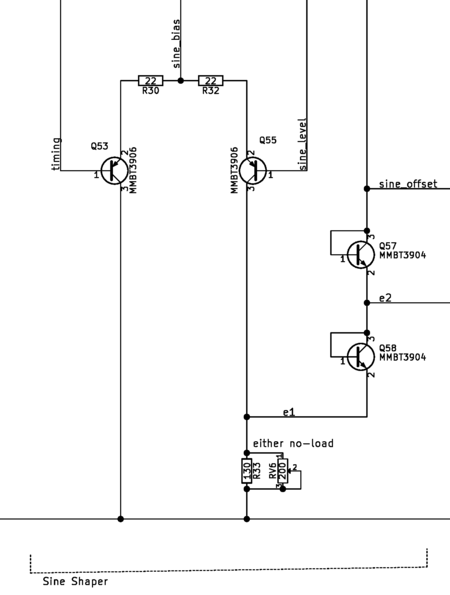
Sine Shaping
The sine shaping circuit distorts the triangle wave from the function generator into a tanh, a sine wave approximation. It uses the triangle wave to over drive the shaper's differential pair, causing non-linear distortion near the peaks of the waveform. The circuit "snips" the sharp peaks from the triangle wave, leaving an approximated sine wave.
This sine shaper is difficult to design due the design relying on the non-idealities of the transistors in the differential pair. For the most part, this shaper circuit is designed experimentally. There exists more controlled circuits, such as the typical piece-wise sine-shaping technique that uses more than 10 or more shaping diodes to accurately shape the waveform. I chose to use the simplicity of the differential pair sine shaper over the piecewise topology, since I had to build this circuit by hand.
The shaper circuit is not only difficult to design but also highly susceptable to inaccuracies in its input, inacGcuracies in its biasing, and temperature. As a result, this sine shaper is just a novelty circuit that produces merely an approximation of a sine wave.
The amount of distortion, set by the tail bias current, must be tuned the amplitude of the triangle wave input. In typical operation of the function generator, the triangle wave's amplitude changes slightly with frequency, so the distortion varies slightly with frequency.
Mismatch between the sine shaper's offset reference and the input waveform's offset causes the sine shaper to distort the triangle wave asymmetrically. A problem with this constraint is that the triangle wave's offset changes with temperature, by the design of the Schmitt trigger. To solve this problem, I intentionally "pre-distort" the shaper's offset reference with temperature sensitive diodes so that it matches the temperature change produced by the Schmitt trigger. The Schmitt trigger's waveform offset changes with the voltage of the two active diodes in its feedback loop, so I created a circuit to provide a voltage reference that depends on the voltage of two active diodes. In this way, I compensated for temperature sensitivity of the shaper's symmetry.
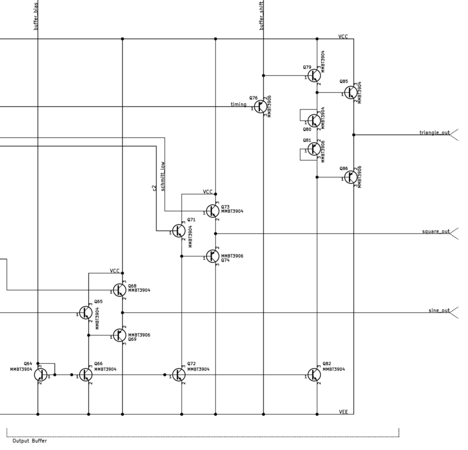
Output Stages
The function generator has dedicated output buffers for each of the three waveforms. The amplifiers are class AB emitter push-pull circuits. Although the circuits are technically class AB, they have been biased more towards class A to minimize crossover distortion and to improve frequency response.
The buffers for the sine and square wave are special in that they reuse the voltage offset diode inside inside the circuits they are buffering. Normally, two diode voltage drops are needed to convert a class B push-pull amplifier to a class AB amplifier. The two diodes also need a common-collector prebuffer to drive them, which changes the output waveform's offset to an inconvenient level. By reusing a diode voltage drop from the buffered circuits, I lower the transistor count and avoid additional complexity.
The buffer for the triangle wave was constructed in the more typical way, since there was no existing diode voltage drop for it to use. This buffer also has additional circuitry to perform a level shift so that its output waveform offset matches that of the other buffers.
Design Methodology
Although the focus of the FGC-200 project is electronic hardware, much of the work was done in software in the form of automated design and simulation. On a design involving 86 transistors, iterating the design by hand would trigger flashbacks to my days of late-night university homework cram sessions. In addition to automation, a key to designing a large system is to design and test in small parts before integrating them together. The human brain can only do and remember so much.
Automated Design with Python
Having every part of the system affect every other part of the system is an inevitable feature of analog design. As a result of this predicament, I divided up the function generator into subsystems and implemented mathematical design models for each subsystem in Python programming.
The design models mapped given desired output characteristics of a subsystem to the internal configuration of the subsystem. Internal configuration includes attributes like biasing, component values, or subtle topology changes. The models themselves also verified that the given inputs produced valid designs, so I didn't need worry about design mistakes myself.
The models for the subsystems could be instantiated separately with given inputs, a capability that allows me to chain together or duplicate subsystem models to produce a larger model for full system automated design. In addition to producing a large design model, the instantiation allowed me to easily create different designs for comparison.
Circuit Simulation with SPICE
Following the automated design, I implemented SPICE circuit models of each subsystem with the parameters found using the automated design program. Like the automated design program, the function generator circuit model was divided into many subsystems that could be operated independently.
Each subsystem model also had an ideal test circuit that represented the environment the subsystem would be used in. This test circuit is known as a "test bench" in the hardware world or a "unit test" in the software world. The ideal test circuits allowed me to gain confidence in and iterate on the design of a subsystem without worrying about the rest of the system. As a result of this method, I abstracted alway the details of subsystem internals and obtained design confidence at the subsystem level. I could reliably integrate the whole system together to perform full simulations of the entire function generator.
The simulated results from SPICE are compared with the results from the Python design model to ensure that the models match. Note that even with simulation there are non-idealities with the electronic components that cause the results to be slightly different from that of the ideal design model.
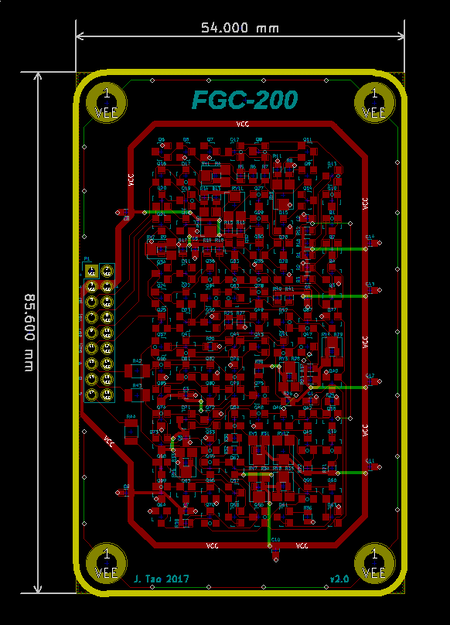
Printed Circuit Board Design
The printed circuit board (PCB) was designed using a 2-layer 0.8 mm thick FR4 board. All components were placed on the front side, along with most of the traces. In this way, the back side was preserved as an unbroken ground plane to complement the traces on the top, a technique that lowers trace inductance at high frequencies. Because there was no room for the power rail near the center of the board, it had to be placed in a ring around the circuit, bridging toward the center of the circuit from the back side.
Although the circuit was supposed to reflect the integrated design style, the physical dimensions and materials used are quite different from a silicon wafer. The large scale of this circuit meant that trace inductance is significant. Decoupling capacitors were a requirement, going against what is capable or necessary within an integrated circuit.
Another difference with the PCB is its thermal resistivity compared to silicon. Differential circuits and temperature compensation circuits, like the bandgap reference, require tight coupling of the components because they compare the behavior between components. A temperature difference between components would add an unwanted difference to those comparisons. In textbooks, these circuits are described with the assumption that the silicon substrate would thermally couple the components together.
In the light of this thermal limitation, I placed related transistor pairs close together and far away from sources of heat to prevent the pairs' temperature from drifting apart. I could cause various circuit characteristics to drift by placing a warm finger on one of the transistors in a pair. Interestingly, the characteristics don't drift if I place a warm finger on both transistors of a pair, which demonstrates the impact of temperature differences. Ultimately, care with thermal coupling resulted in improved frequency stability.
Detriments
The function generator has detriments in its waveform shape and in its practicality in application. These detriments are inherent to the topology.
The triangle wave amplitude changes with frequency, since the Schmitt trigger is not able to switch the timing currents quickly enough. As the frequency increases toward the limit of the trigger's response speed limit, the waveform's amplitude overshoots the trigger's threshold for the time it takes the trigger to respond. This behavior also makes frequency programming of the function generator inaccurate.
The sine wave shape distorts severely with the triangle wave's amplitude and frequency. Much of the distortion comes from the changing amplitude of the trinagle wave as previously described. Also, the sine shaper's frequency response is also limited, which causes its amplitude to greatly drop after around 30 MHz.
In a practical application, the timing capacitor is placed off of the main board. This introduces a series inductance with the timing capacitor and creates an unintended resonant circuit. Oscillation in this resonant circuit starts when the function generator switches the charging currents. The high impedance of the current sources used to charge the timing capacitor allows the voltage oscillation on the timing capacitor to ring with little damping. A solution to the oscillation problem is to place a small damping resistor, about 10 Ω, in series with the timing capacitor.
This series resistance improvement can eliminate the oscillation, but it introduces a voltage offset due to charging current flowing through this resistance. The voltage offset can be severe enough to reduce the tuning range of the function generator, because high frequencies ranges need higher charging currents.
The ultimate solution to the oscillation would be to eliminate the parasitic inductance of the conductor going from the function generator's current switch to the capacitor. Soldering the timing capacitor directly to the function generator can reduce much of the oscillation, but it is not practical to a user. On top of that, oscillation may still occur due to the capacitor's self-resonance. Perhaps this is a big reason why RC-based oscillators are no longer a popular solution for test instruments that need to produce pristine waveforms.
Cost to Prototype and Manufacture
The cost for prototyping materials was US $81.77, which includes the cost of components from multiple units with extras, PCB fabrication, taxes, shipping, and other fabrication goodies like solder paste stencils. Thanks to the rigorous design process, only one payment of this prototyping cost was needed to make a working circuit.
At the 10 unit scale, the raw cost of the components alone amounts to US $7.72, while the PCB cost is about $2. It's safe to say that the FGC-200 is a $10 function generator.
The labor cost of assembly is extremely high. Although I have a reflow oven and stencil to save time on soldering, I don't have a machine to place the 157 parts onto the board for soldering. The board takes about two hours to assemble. At a hypothetical wage of about US $10 per hour, the FGC-200 costs $20 to assemble. The inclusion of labor cost brings the cost of the unit to about $30.